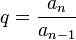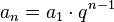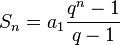Ova stranica je u izradi…
DERIVACIJA FUNKCIJE f u točki x0
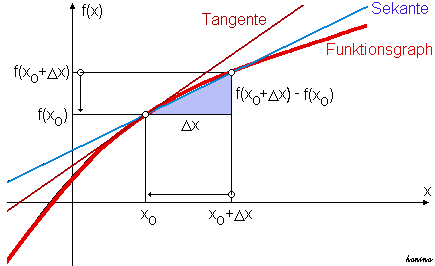
Tangenta je pravac koji dodiruje krivulju u jednoj točki.
Na svaku je krivulju npr. kružnicu, elipsu, parabolu, hiperbolu moguće položiti beskonačno mnogo tangenata, ali kroz svaku točku glatke krivulje prolazi samo jedna tangenta
Jednadžba pravca tangente je y – y0 = k(x – x0),
pri čemu je koeficijent smjera k jednak derivaciji funkcije krivulje u točki x0 odnosno
k = f’(x0).
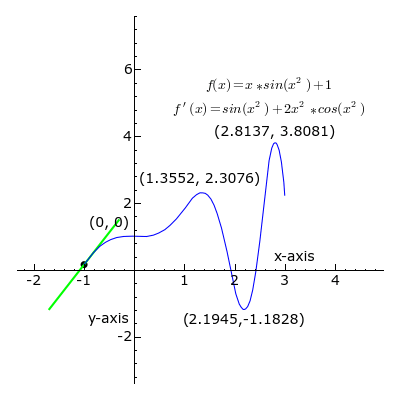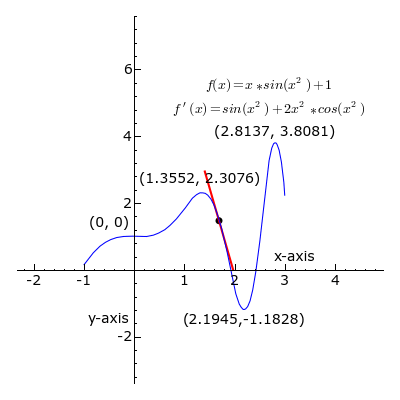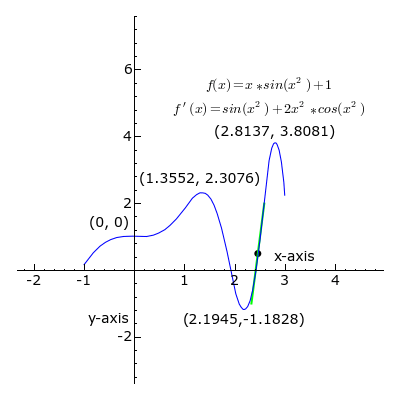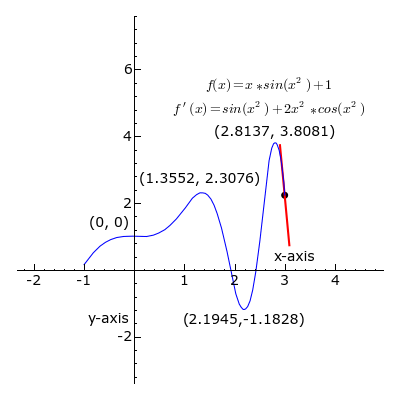
Na animiranoj slici (iznad) prikazana je krivulja složene funkcije:
f(x) = xsin(x2) + 1
u dvodimenzionalnom koordinatnom sustavu (x,y).
U svakoj točki krivulje (u intervalu od x = -1 do x = 3) prikazana je tangenta na krivulju.
– Kada je koeficijent smjera tangente (odnosno prva derivacija funkcije) pozitivan, k > 0,
dio pravca tangente je zelene boje.
– Kada je koeficijent smjera tangente negativan, k < 0,
dio pravca tangente je crvene boje.
– Kada je koeficijent smjera tangente jednak nuli, k = 0,
tj. kad funkcija ima lokalni ekstrem (minimum ili maksimum),
dio pravca tangente je crne boje.
Izvor: wikipedija
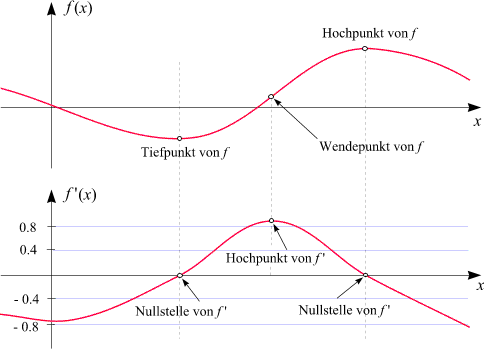
FUNKCIJA f
označene su točke:
- minimuma
- infleksije
- maksimuma
DERIVACIJA FUNKCIJE f’
označene su točke:
- nultočka
- maksimum
- nultočka
Možete se poslužiti sadržajem NIZOVI I REDOVI iz udžbenika preuzetog s linka: https://element.hr/artikli/file/1213
Dodatni materijali za rad:
- Teorija i zadaci: NIZ; ARITMETIČKI NIZ
http://www.alkascript.hr/index.php/katalog-proizvoda/srednje-skole/trgovacka-skola?format=raw&task=download&fid=200 - Dodatne zadatke za vježbu možete pogledati na linku: http://www.gssjd.hr/wp-content/uploads/2010/11/DZ1_4r_RM-1.pdf
Navedeni dokumenti su priloženi i u pdf obliku.
Aritmetički niz je niz za koji vrijedi da je razlika susjednih članova niza konstantna. Ta razlizka se označava s d.
![]()
Aritmetički niz je niz oblika:
![]()
Da bismo formirali aritmetički niz moramo poznavati a1 i d
Za opći član niza vrijedi:

Svaki član aritmetičkog niza je aritmetička sredina njemu susjednih članova niza, tj.

Zbroj prvih n članova niza je

Geometrijski niz je niz brojeva kod kojeg je količnik svakog člana i člana ispred njega uvijek stalan broj. Taj broj označavamo sa q i nazivamo ga kvocijentom, a računamo ga pomoću formule:
Da bismo formirali geometrijski niz moramo poznavati a1 i q
Opći član geometrijskog niza koji ima beskonačno elemenata:
Zbroj konačno mnogo članova geometrijskog niza:
Svaki član geometrijskog niza, osim prvog, je geometrijska sredina dvaju susjednih članova.



Što ćeš naučiti?
- Kako nastaje graf funkcije f(x) = sin x
- Kako nastaje graf funkcije f(x) = COS x
Klikom na gumbove Start i Stop možeš pokrenuti, odnosno zaustaviti animaciju. Dok je animacija zaustavljena, možeš povlačiti točku u koordinatnom sustavu.
U kojim je točkama vrijednost funkcije sinus jednaka 0 ?
Kolika je funkcijska vrijednost u točki s apscisom .png) ?
?
Provjeri što se događa ako povlačiš točku A po kružnici?
Graf funkcije f(x)=asin(bx+c)+d
Namatanje brojevnog pravca na BROJEVNU KRUŽNICU
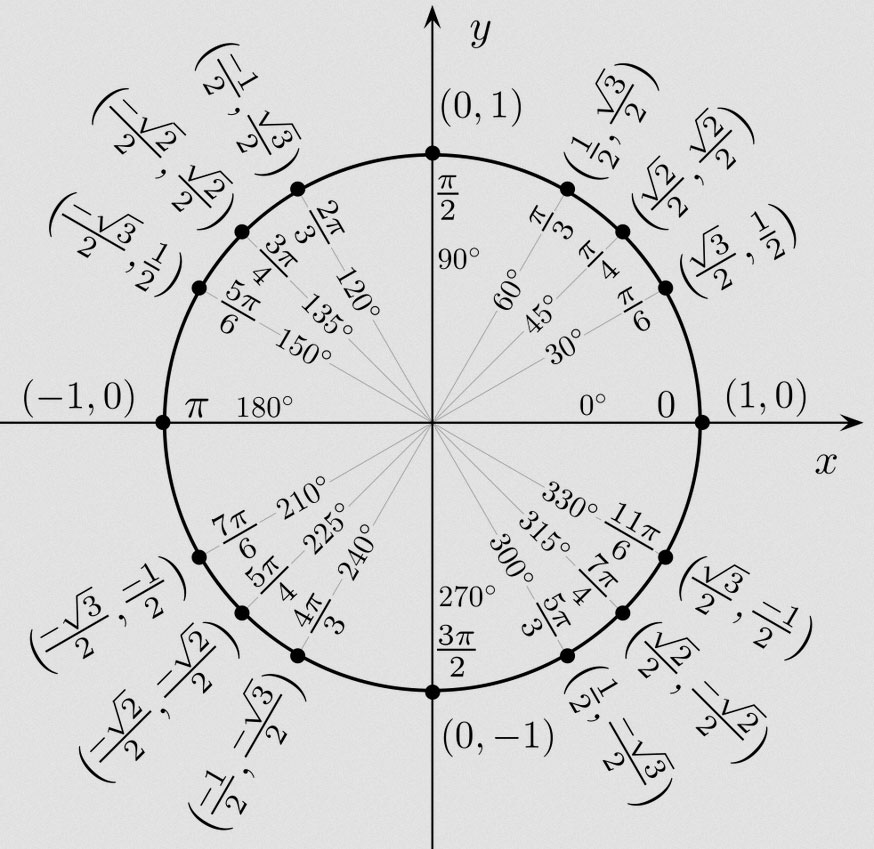
Formule redukcije se nalaze u priloženim datotekama
Danas ćemo
- mjeriti duljine i izračunavati omjere visine i širine papira
- računati izraze s korijenima
- procjeniti i izračunati vrijednost drugoga korijena služeći se džepnim računalom
- ponoviti razliku između racionalnih i iracionalnih brojeva
- istražiti svojstva standardnih formata papira
(OBRAZOVNI ISHODI)
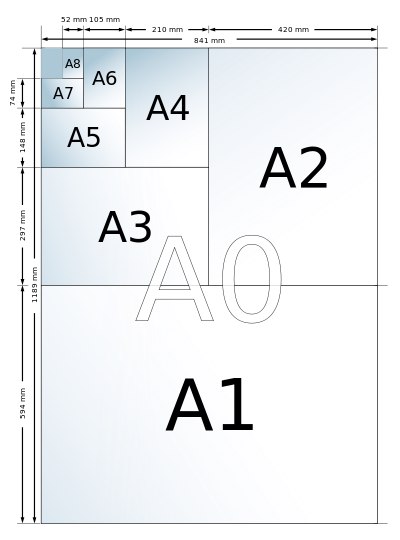
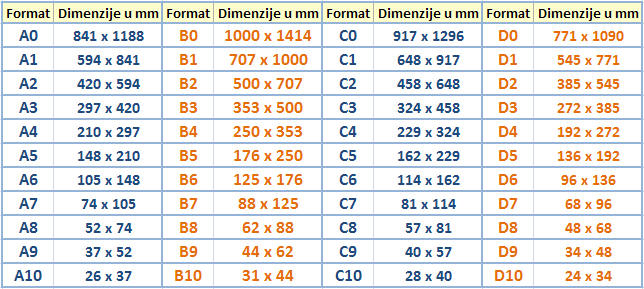
ZADACI:
- Izmjeri dimenzije i pokušaj odrediti format nekih "papira" kod kuće (primjerice: osobna iskaznica, pokaz, putovnica, igraće karte, udžbenik iz matematike, omiljena knjiga…).
Dozvoljena je tolerancija ±1.5 mm za dimenzije do 150 mm,
±2 mm za dimenzije od 150 mm do 600 mm i ±3 mm za dimenzije iznad 600 mm. - Koliko posto treba na fotokopirnom aparatu uvećati sliku želimo li papir formata A5 kopirati na format A4?
- Na pakiranju A4 papira stoji da on teži 80 g/m2. Na kartonskoj uredskoj ladici stoji da je predviđena za težine do 2 kg.
Možemo li u nju staviti cijeli paket od 500 papira? - Koliko bi puta (teoretski) trebao/la presavinuti papir na pola da njegova debljina dosegne tvoju visinu?
- Pogledaj video The A4 Paper Puzzle i riješi zadatak zadan u njemu.
- Može li se presavijanjem papira doći do mjeseca?
Kako možemo doći do Mjeseca savijajući papir - Koliko se puta stvarno može presaviti papir?
MythBusters- Folding Paper Seven plus times - Što se dogodi s papirom ako se presavije jednom previše?
Watch What Happens When You Use A Hydraulic Press To Try To Fold A Piece Of Paper Seven Times - Kako presavijanjem papira do korijena broj 2 i kako dokazati da je on iracionalan broj?
Root 2 – Numberphile
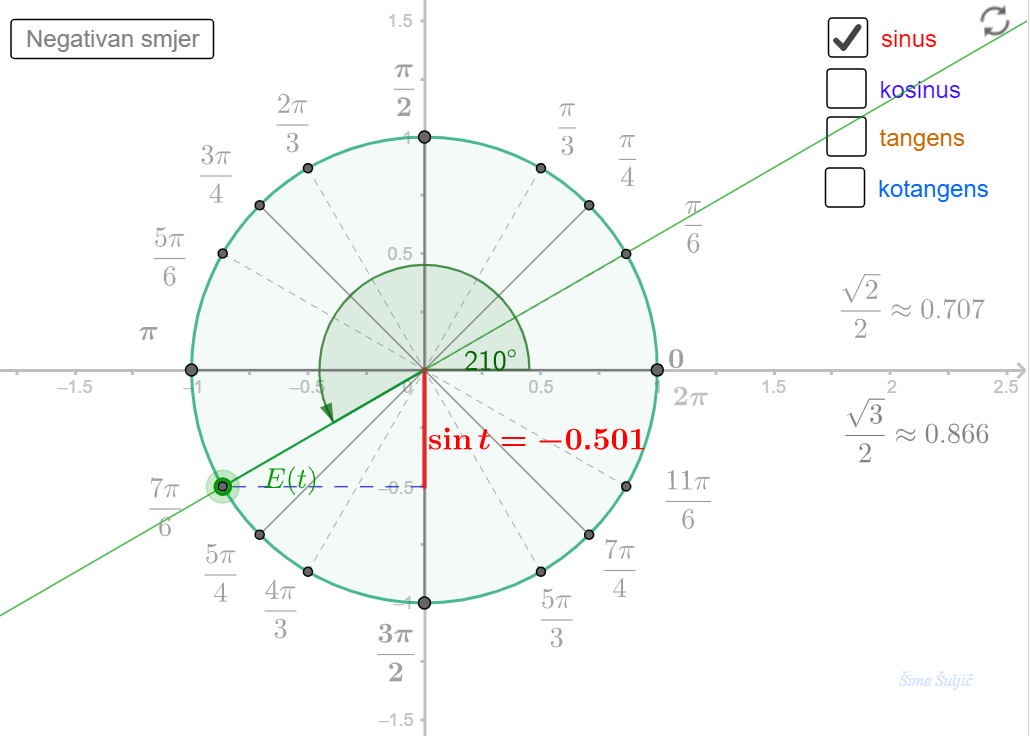
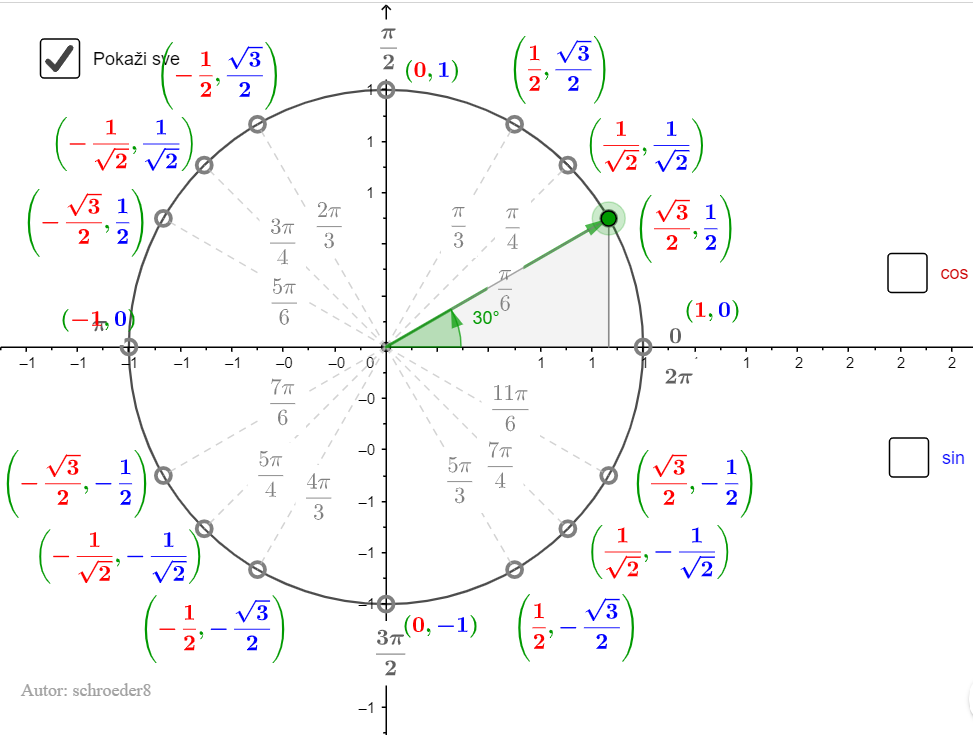
Vrijednosti trigonometrijskih funkcija
- Autor:
- Vesna Josipović, Šime Šuljić
- Tema:
- Kosinus, Sinus, Trigonometrija
POVEZNICA NA 1. APLET U GEOGEBRI
Vrijednosti sinusa i kosinusa istaknutih kutova
- Autor:
- Vesna Josipović, Šime Šuljić
- Tema:
- Kosinus, Sinus, Trigonometrija
POVEZNICA NA 2. APLET U GEOGEBRI
Vrijednost sinusa i kosinusa kuta između 90° i 180°
https://www.geogebra.org/m/pkjzmd5u#material/hqgkx4ee
http://sinusov-poucak.weebly.com/primjeri-iz-geogebre-1.html#
Četiri krivulje drugog reda, kružnice, elipse, parabole ili hiperbole mogu se dobiti promjenom nagiba ravnine kojom presijecamo konus (tj. promjenom kuta između osi konusa i ravnine koja ga presijeca). U geogebrinom apletu (ispod ovog teksta) razmatramo beskonačni stožac s kutom α (kut između izvodnice stošca i osi stošca).
Poigrajte se animacijom kako biste vidjeli demonstraciju konika (krivulja drugog reda):
- hiperbole
- parabole
- elipse
- kruga
Zaustavite animaciju i istražite dodatne posebne slučajeve promjenom:
- kuta ravnine (povucite narančastu točku)
- položajem ravnine (povucite smeđu točku)
- kutom α (kut između izvodnice stošca i osi stošca)
Ovisno o tome pod kojim kutem ravnina presjeca ovaj beskonačni stožac, imamo sljedeće situacije:
- ako je kut između ravnine i osi stošca 0° imamo DVA PRAVCA
- ako je kut između ravnine i osi stošca veća od 0° i manja od α imamo HIPERBOLU
- ako je kut između ravnine i osi stošca veća od α manja od 90° imamo ELIPSU
- ako je kut između ravnine i osi stošca 90° imamo KRUŽNICU
KONSTRUKCIJA PARABOLE metodom presavijanja papira
DODATAK – možete pogledati i ove geogebrine aplete:
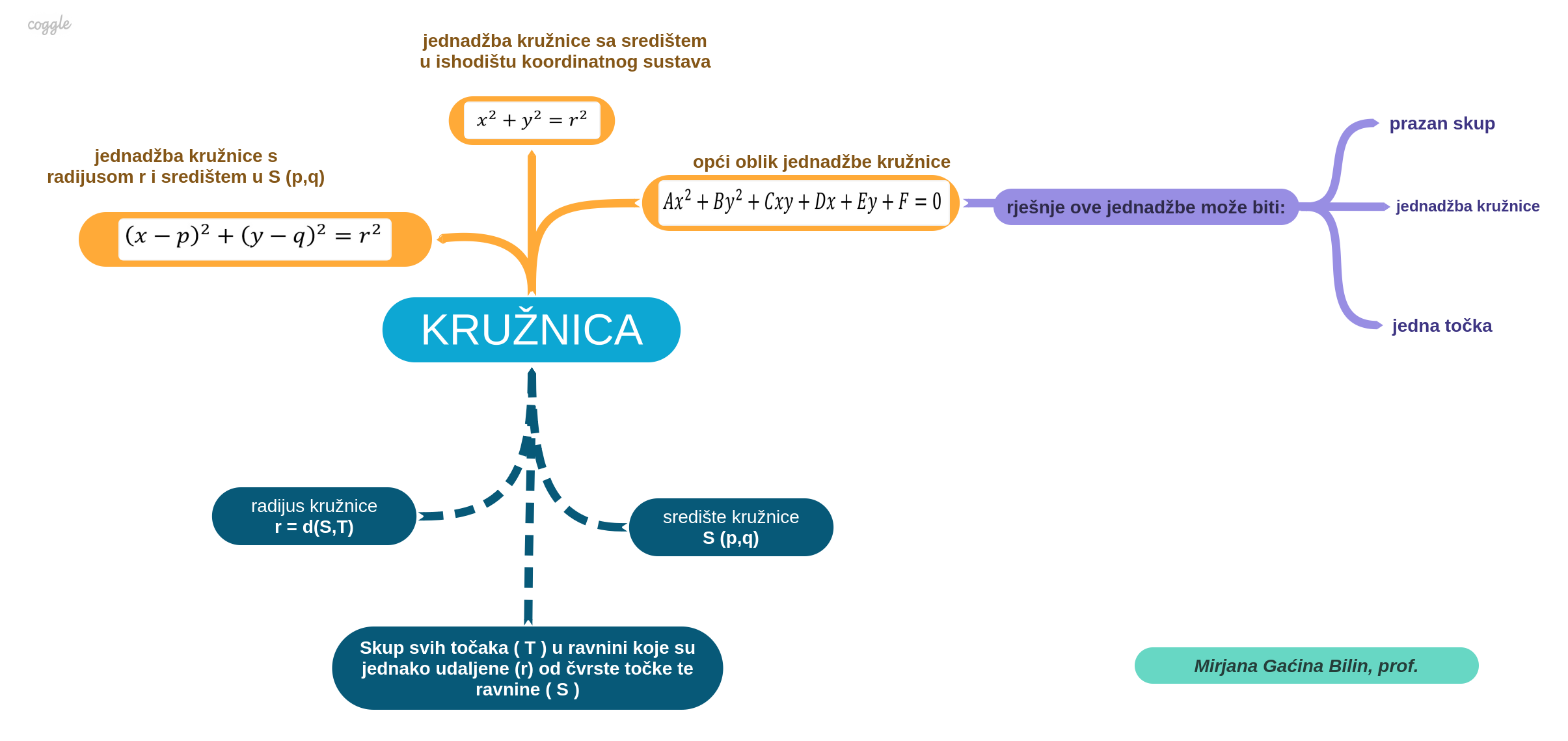
Ponovimo zajedno igrajući se zadacima u geogebri:
Kružnica kroz zadanu točku, koja dodiruje obje osi
Međusobni položaj dviju kružnica (1)
SISTEMATIZACIJA GRADIVA
Uputa:
Riješite zadatke s listića u priloženom dokumentu zadaci za vjezbu – kruznica.pdf. Rješenja možete provjeriti ovdje u apletima Geogebre. U njima su nacrtane sve kružnice, a vi možete dodavati i konstruirati sve što je potrebno za provjeru vaših rješenja.
- Prikazati vektore u ravnini
- Zbrajati ih i oduzimati
- Množiti vektore sa skalarom
- Primijeniti vektore i operacije s njima za prikazivanje i istraživanje geometrijskih oblika
ZA ŠTO MI TO TREBA?
- Za određivanje rezultantne sile
- Za određivanje smjera kretanja zrakoplova
- Za određivanje brzine kretanja zrakoplova u odnosu na tlo
SVOJSTVA VEKTORA:


Matematika 3, II.dio, udžbenik za 3. razred četverogodišnje strukovne škole
I.Čavlović, M.Lapaine
Školska knjiga, Zagreb, 2005
ZBRAJANJE VEKTORA
ODUZIMANJE VEKTORA
ZBRAJANJE I ODUZIMANJA VEKTORA – PRAVILA
CRTANJE VEKTORA U KOORDINATNOM SUSTAVU
KOLINEARNI VEKTORI
MNOŽENJE VEKTORA SKALAROM
POGLEDAJTE VIDEO SA SKRIVENIM ZADACIMA

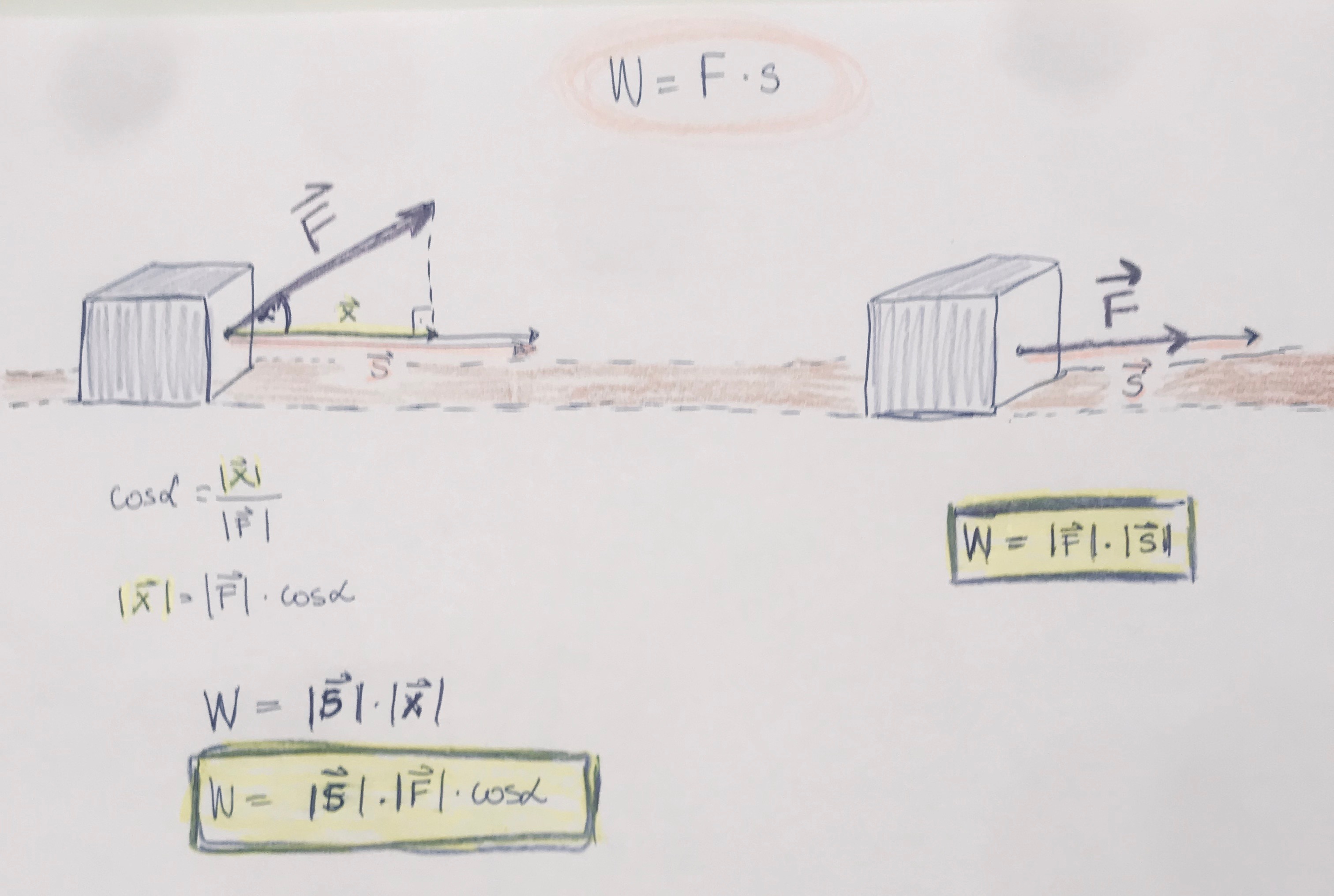
RAD JE SAVLADAVANJE (djelovanje) SILE NA NEKOM PUTU.
Kolika je sila potrebna da bi se uz isti rad tijelo na slikama pokmaklo za isti put?
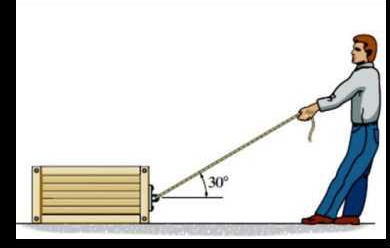
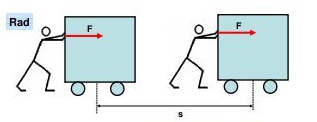
Skalarni produkt dvaju vektora jest SKALAR (realan broj) koji je jednak umnošku modula tih vektora i kosinusa kuta između njih
SVOJSTVA:

Matematika 3, II.dio, udžbenik za 3. razred četverogodišnje strukovne škole
I.Čavlović, M.Lapaine
Školska knjiga, Zagreb, 2005
Zadana su dva vektora i kut među njima:
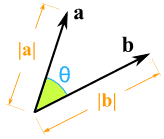
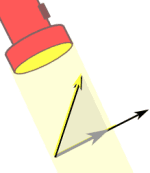
Ortogonalna projekcija dužine a na pravac nosioc vektora  nazivamo SKALARNA PROJEKCIJA vektora
nazivamo SKALARNA PROJEKCIJA vektora 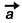 na vektor
na vektor 
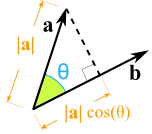
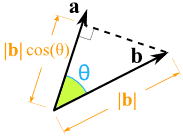
Provjeri pomoću skalarnog produkta valjanost podataka sa slike:

PRVI RAZRED
Smjer: farmaceutski tehničar
MATEMATIKA – projektni zadatak
Matematika u egipatskim piramidama i zvjezdanom nebu
MATEMATIKA – projektni zadatak
Primjena trigonometrije u raznim aspektima života.
Vrijednosti trigonometrijskih funkcija
- Tema:
- Kosinus, Sinus, Trigonometrija
POVEZNICA NA 1. APLET U GEOGEBRI
Vrijednosti sinusa i kosinusa istaknutih kutova
- Tema:
- Kosinus, Sinus, Trigonometrija
POVEZNICA NA 2. APLET U GEOGEBRI
Vrijednost sinusa i kosinusa kuta između 90° i 180°
https://www.geogebra.org/m/pkjzmd5u#material/hqgkx4ee
http://sinusov-poucak.weebly.com/primjeri-iz-geogebre-1.html#
Priloženi dokumenti:![]()
![]() POUCAK O SINUSU ZADACI.pdf
POUCAK O SINUSU ZADACI.pdf![]()
![]() Zadatci – Poucak o sinusima 2-dio.pdf
Zadatci – Poucak o sinusima 2-dio.pdf
DERIVACIJA FUNKCIJE f u točki x0

Tangenta je pravac koji dodiruje krivulju u jednoj točki.
Na svaku je krivulju npr. kružnicu, elipsu, parabolu, hiperbolu moguće položiti beskonačno mnogo tangenata, ali kroz svaku točku glatke krivulje prolazi samo jedna tangenta
Jednadžba pravca tangente je y – y0 = k(x – x0),
pri čemu je koeficijent smjera k jednak derivaciji funkcije krivulje u točki x0 odnosno
k = f’(x0).
Na animiranoj slici (iznad) prikazana je krivulja složene funkcije:
f(x) = xsin(x2) + 1
u dvodimenzionalnom koordinatnom sustavu (x,y).
U svakoj točki krivulje (u intervalu od x = -1 do x = 3) prikazana je tangenta na krivulju.
– Kada je koeficijent smjera tangente (odnosno prva derivacija funkcije) pozitivan, k > 0,
dio pravca tangente je zelene boje.
– Kada je koeficijent smjera tangente negativan, k < 0,
dio pravca tangente je crvene boje.
– Kada je koeficijent smjera tangente jednak nuli, k = 0,
tj. kad funkcija ima lokalni ekstrem (minimum ili maksimum),
dio pravca tangente je crne boje.
Izvor: wikipedija


FUNKCIJA f
označene su točke:
- minimuma
- infleksije
- maksimuma
DERIVACIJA FUNKCIJE f’
označene su točke:
- nultočka
- maksimum
- nultočka
Možete se poslužiti sadržajem NIZOVI I REDOVI iz udžbenika preuzetog s linka: https://element.hr/artikli/file/1213
Dodatni materijali za rad:
- Teorija i zadaci: NIZ; ARITMETIČKI NIZ
http://www.alkascript.hr/index.php/katalog-proizvoda/srednje-skole/trgovacka-skola?format=raw&task=download&fid=200 - Dodatne zadatke za vježbu možete pogledati na linku: http://www.gssjd.hr/wp-content/uploads/2010/11/DZ1_4r_RM-1.pdf
Navedeni dokumenti su priloženi i u pdf obliku.
Aritmetički niz je niz za koji vrijedi da je razlika susjednih članova niza konstantna. Ta razlizka se označava s d.
![]()
Aritmetički niz je niz oblika:
![]()
Da bismo formirali aritmetički niz moramo poznavati a1 i d
Za opći član niza vrijedi:

Svaki član aritmetičkog niza je aritmetička sredina njemu susjednih članova niza, tj.

Zbroj prvih n članova niza je

Geometrijski niz je niz brojeva kod kojeg je količnik svakog člana i člana ispred njega uvijek stalan broj. Taj broj označavamo sa q i nazivamo ga kvocijentom, a računamo ga pomoću formule:
Da bismo formirali geometrijski niz moramo poznavati a1 i q
Opći član geometrijskog niza koji ima beskonačno elemenata:
Zbroj konačno mnogo članova geometrijskog niza:
Svaki član geometrijskog niza, osim prvog, je geometrijska sredina dvaju susjednih članova.
Četiri krivulje drugog reda, kružnice, elipse, parabole ili hiperbole mogu se dobiti promjenom nagiba ravnine kojom presijecamo konus (tj. promjenom kuta između osi konusa i ravnine koja ga presijeca). U geogebrinom apletu (ispod ovog teksta) razmatramo beskonačni stožac s kutom α (kut između izvodnice stošca i osi stošca).
Poigrajte se animacijom kako biste vidjeli demonstraciju konika (krivulja drugog reda):
- hiperbole
- parabole
- elipse
- kruga
Zaustavite animaciju i istražite dodatne posebne slučajeve promjenom:
- kuta ravnine (povucite narančastu točku)
- položajem ravnine (povucite smeđu točku)
- kutom α (kut između izvodnice stošca i osi stošca)
Ovisno o tome pod kojim kutem ravnina presjeca ovaj beskonačni stožac, imamo sljedeće situacije:
- ako je kut između ravnine i osi stošca 0° imamo DVA PRAVCA
- ako je kut između ravnine i osi stošca veća od 0° i manja od α imamo HIPERBOLU
- ako je kut između ravnine i osi stošca veća od α manja od 90° imamo ELIPSU
- ako je kut između ravnine i osi stošca 90° imamo KRUŽNICU
KONSTRUKCIJA PARABOLE metodom presavijanja papira
DODATAK – možete pogledati i ove geogebrine aplete:

Ponovimo zajedno igrajući se zadacima u geogebri:
Kružnica kroz zadanu točku, koja dodiruje obje osi
Međusobni položaj dviju kružnica (1)
SISTEMATIZACIJA GRADIVA
Uputa:
Riješite zadatke s listića u priloženom dokumentu zadaci za vjezbu – kruznica.pdf. Rješenja možete provjeriti ovdje u apletima Geogebre. U njima su nacrtane sve kružnice, a vi možete dodavati i konstruirati sve što je potrebno za provjeru vaših rješenja.
Priloženi dokumenti:![]()
![]() zadaci za vjezbu – kruznica.pdf
zadaci za vjezbu – kruznica.pdf![]()
![]()
![]() umna pama – KRUzNICA.pdf
umna pama – KRUzNICA.pdf![]()
![]() KRUZNICA uvodno predavanje.pdf
KRUZNICA uvodno predavanje.pdf
- Prikazati vektore u ravnini
- Zbrajati ih i oduzimati
- Množiti vektore sa skalarom
- Primijeniti vektore i operacije s njima za prikazivanje i istraživanje geometrijskih oblika
ZA ŠTO MI TO TREBA?
- Za određivanje rezultantne sile
- Za određivanje smjera kretanja zrakoplova
- Za određivanje brzine kretanja zrakoplova u odnosu na tlo
SVOJSTVA VEKTORA:


Matematika 3, II.dio, udžbenik za 3. razred četverogodišnje strukovne škole
I.Čavlović, M.Lapaine
Školska knjiga, Zagreb, 2005
ZBRAJANJE VEKTORA
ODUZIMANJE VEKTORA
ZBRAJANJE I ODUZIMANJA VEKTORA – PRAVILA
CRTANJE VEKTORA U KOORDINATNOM SUSTAVU
KOLINEARNI VEKTORI
MNOŽENJE VEKTORA SKALAROM
POGLEDAJTE VIDEO SA SKRIVENIM ZADACIMA
Priloženi dokumenti:![]() vektori ZADACI ZA VJEZBU.docx
vektori ZADACI ZA VJEZBU.docx

RAD JE SAVLADAVANJE (djelovanje) SILE NA NEKOM PUTU.
Kolika je sila potrebna da bi se uz isti rad tijelo na slikama pokmaklo za isti put?


Skalarni produkt dvaju vektora jest SKALAR (realan broj) koji je jednak umnošku modula tih vektora i kosinusa kuta između njih
SVOJSTVA:

Matematika 3, II.dio, udžbenik za 3. razred četverogodišnje strukovne škole
I.Čavlović, M.Lapaine
Školska knjiga, Zagreb, 2005
Zadana su dva vektora i kut među njima:


Ortogonalna projekcija dužine a na pravac nosioc vektora  nazivamo SKALARNA PROJEKCIJA vektora
nazivamo SKALARNA PROJEKCIJA vektora  na vektor
na vektor 


Provjeri pomoću skalarnog produkta valjanost podataka sa slike:

Što ćeš naučiti?
- Kako nastaje graf funkcije f(x) = sin x
- Kako nastaje graf funkcije f(x) = COS x
Klikom na gumbove Start i Stop možeš pokrenuti, odnosno zaustaviti animaciju. Dok je animacija zaustavljena, možeš povlačiti točku u koordinatnom sustavu.
U kojim je točkama vrijednost funkcije sinus jednaka 0 ?
Kolika je funkcijska vrijednost u točki s apscisom .png) ?
?
Provjeri što se događa ako povlačiš točku A po kružnici?
Namatanje brojevnog pravca na BROJEVNU KRUŽNICU

Formule redukcije se nalaze u priloženim datotekama
Priloženi dokumenti:![]()
![]() Prilog-Formule-redukcije.pdf
Prilog-Formule-redukcije.pdf![]()
![]() Prilog-Formule-redukcije-1.pdf
Prilog-Formule-redukcije-1.pdf
Danas ćemo
- mjeriti duljine i izračunavati omjere visine i širine papira
- računati izraze s korijenima
- procjeniti i izračunati vrijednost drugoga korijena služeći se džepnim računalom
- ponoviti razliku između racionalnih i iracionalnih brojeva
- istražiti svojstva standardnih formata papira
(OBRAZOVNI ISHODI)


ZADACI:
- Izmjeri dimenzije i pokušaj odrediti format nekih “papira” kod kuće (primjerice: osobna iskaznica, pokaz, putovnica, igraće karte, udžbenik iz matematike, omiljena knjiga…).
Dozvoljena je tolerancija ±1.5 mm za dimenzije do 150 mm,
±2 mm za dimenzije od 150 mm do 600 mm i ±3 mm za dimenzije iznad 600 mm. - Koliko posto treba na fotokopirnom aparatu uvećati sliku želimo li papir formata A5 kopirati na format A4?
- Na pakiranju A4 papira stoji da on teži 80 g/m2. Na kartonskoj uredskoj ladici stoji da je predviđena za težine do 2 kg.
Možemo li u nju staviti cijeli paket od 500 papira? - Koliko bi puta (teoretski) trebao/la presavinuti papir na pola da njegova debljina dosegne tvoju visinu?
- Pogledaj video The A4 Paper Puzzle i riješi zadatak zadan u njemu.
- Može li se presavijanjem papira doći do mjeseca?
Kako možemo doći do Mjeseca savijajući papir - Koliko se puta stvarno može presaviti papir?
MythBusters- Folding Paper Seven plus times - Što se dogodi s papirom ako se presavije jednom previše?
Watch What Happens When You Use A Hydraulic Press To Try To Fold A Piece Of Paper Seven Times - Kako presavijanjem papira do korijena broj 2 i kako dokazati da je on iracionalan broj?
Root 2 – Numberphile
Pokušajte riješiti što više …..
Malo znanja ljude čini dobrima, a mnogo skromnima.
Leonardo da Vinci
Naoružajte se kavom, strpljenjem i upornošću! Provjerena formula ![]()
Samo rad će vas dovesti do uspjeha! Na linku koji sljedi ćete pronaći puuuuuno korisnih i što je još važnije, riješenih zadataka.
DOSADAŠNJI, RIJEŠENI ISPITNI ROKOVI
http://web.vip.hr/robert.gortan.vip/nastava_matematike.html
Sretno!
Vaša prof. M.G.B.
U priloženim dokumentima ćete pronaći materijale pomoću kojih možete ponoviti obrađene sadržaje.
Priloženi dokumenti:![]()
![]() Elipsa.ppt
Elipsa.ppt![]()
![]() ELIPSA 2.ppt
ELIPSA 2.ppt